Laboratoire hôte :
Laboratoire Hubert Curien (LaHC), 18 Rue Pr B. Lauras, 42000 SAINT-ÉTIENNE.
Laboratoire partenaire :
CEA DAM DIF – 91680 Bruyères-le-Châtel.
Superviseurs et contacts :
Ludovic Chopineau – CEA-DAM (ludovic.chopineau@cea.fr), Fabien Momey Casella – LabHC (fabien.momey@univ-st-etienne.fr).
Mots-clés :
modèles numériques, restauration/reconstruction d’image, problèmes inverses, imagerie computationnelle, imagerie en rayons X, Laser Mégajoule, fusion nucléaire.
Durée et date de démarrage :
4 à 6 mois à partir de février/mars 2026.
Contexte et problématique :
L’étude de la matière soumise à de hautes densités d’énergie est d’un intérêt majeur en perspective des futures expériences de fusion par confinement inertiel prévues sur le Laser Mégajoule (LMJ). Dans le cas d’une implosion par attaque indirecte, il est notamment nécessaire de parfaitement maîtriser les conditions de pression et de température dans la cavité pour atteindre le régime d’ignition. Dans ces régimes extrêmes, les mécanismes physiques mis en jeu peuvent évoluer à l’échelle du μm/ps. L’observation in-situ de tels phénomènes constitue donc un enjeu et défi majeurs. Les dispositifs de mesure employés dans le cadre de ces applications, également appelés diagnostics plasmas, sont dotés pour la plupart d’un microscope X spécifique – bloc optique X à miroir torique simple – permettant d’imager une physique bien définie.
Il est alors fondamental de connaître parfaitement la réponse spatio-spectrale de l’instrument et d’être en capacité de simuler numériquement cette réponse. Disposer d’un tel modèle numérique de formation des observations est l’étape-clé dans l’élaboration d’une méthode de restauration de l’information ciblée – la carte des sources d’émission du flux de rayons X engendré par le processus de fusion – affranchie des effets de l’instrument d’observation. Si la réponse de l’instrument est stationnaire quel que soit le point du champ observé, on peut modéliser le processus par la convolution de l’image recherchée par la réponse impulsionnelle ou Point Spread Function (PSF) en anglais, créant une observation « floutée » de l’image. C’est la connaissance de cette PSF et sa modélisation numérique qui constitue alors l’élément-clé du modèle de simulation.
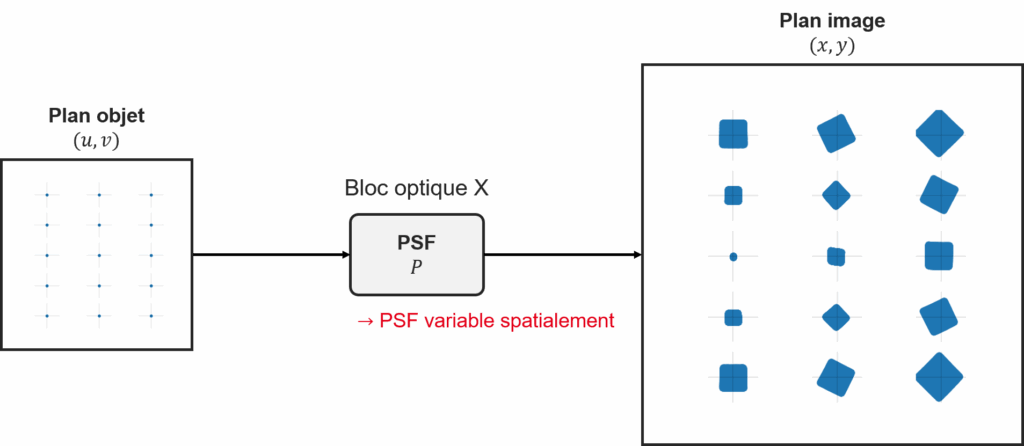
Figure 1. PSF variable dans le champ d’un bloc optique X à miroir torique simple.
Toutefois, le système optique en question dans cette étude présente une réponse spatio-spectrale non-stationnaire, i.e. variable dans le champ et aussi en fonction de la longueur d’onde émise par les sources. Le modèle numérique de formation des observations ne peut donc plus être décrit par une convolution, mais par un opérateur complexe à 4D (cf. Figure 1). Il existe alors plusieurs types d’approches permettant de traiter ce problème inverse dit de « déconvolution variable dans le champ » [1][2][3].
Objectif du stage :
Ce stage est proposé dans le cadre d’une collaboration entre le CEA-DAM Île-de-France et le Laboratoire Hubert Curien de l’Université de Saint-Étienne.
L’objectif de l’étudiant.e recruté consistera à élaborer, à partir de simulations des PSFs obtenues à divers points du champ, un modèle numérique de formation des observations.
Il.Elle devra ensuite exploiter ce modèle dans une méthode numérique de restauration d’image via une approche statistique qui minimise itérativement une fonction de coût composée d’un terme d’adéquation aux observations, impliquant le modèle numérique, et des termes additionnels favorisant les solutions régulières et respectant les contraintes physiques attendues.
La validation de la méthode sera réalisée sur des données issues de simulations. Les résultats obtenus pourront en cas de succès être étendus à l’ensemble des blocs optiques X LMJ.
En fonction de ces résultats, une investigation pourra également être menée sur l’utilisation des atouts de l’apprentissage profond pour enrichir la méthode de restauration.
Formation et compétences souhaitées :
Traitement du signal et de l’image, vision par ordinateur, imagerie computationnelle, deep learning.
Logiciels et compétences techniques : Python, PyTorch, Git (GitLab/Github).
Références
[1] Ralf C. Flicker and François J. Rigaut. Anisoplanatic deconvolution of adaptive optics images. JOSA A, 22(3) :504–513, March 2005. Publisher : Optica Publishing Group.
[2] Elie Maalouf, Bruno Colicchio, and Alain Dieterlen. Fluorescence microscopy three-dimensional depth variant point spread function interpolation using Zernike moments. Journal of the Optical Society of America A, 28 :1864–1870, August 2011.
[3] Loïc Denis, Eric Thiébaut, Ferréol Soulez, Jean-Marie Becker, and Rahul Mourya. Fast Approximations of Shift-Variant Blur. International Journal of Computer Vision, 115(3) :253–278, December 2015.