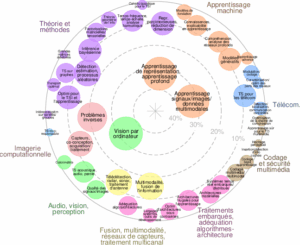
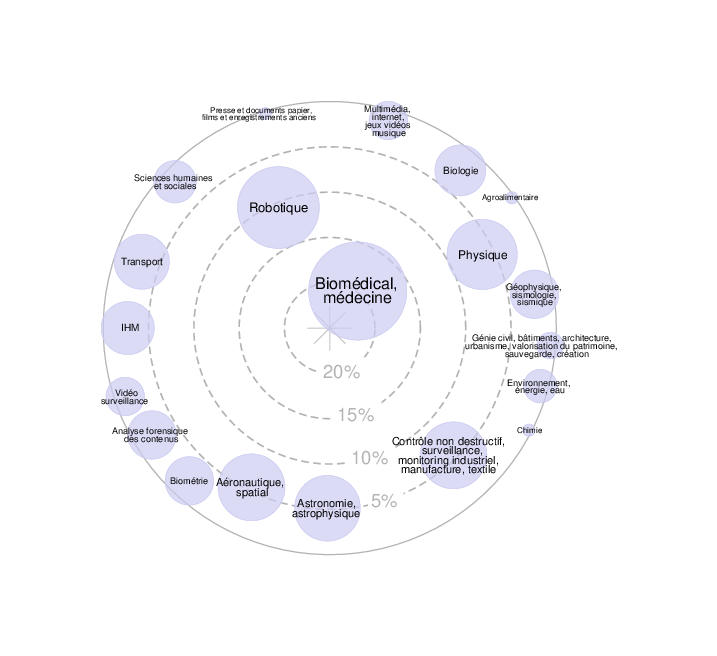
Géométrie de l’information
Depuis quelques années, de nouveaux problèmes ont émergé dans de nombreuses applications liées au traitement du signal et des images où les techniques standards basées sur des résultats d’algèbre linéaire matriciel ne sont plus adaptées ou transposables facilement.
En géométrie de l’information, l’objet d’intérêt (signal, image, vidéo, etc.) est vu comme un point sur un espace métrique (variétés, groupes, etc.) et les problèmes classiques (estimation, filtrage, classification, etc.) doivent être reformulés sur ces espaces qui, en général, possèdent une courbure non nulle. Par exemple, les outils de probabilité et statistique nécessaires à la résolution des problèmes de traitement du signal et des images sont alors définis de manière intrinsèque sur ces espaces courbes. La notion de barycentre ou de mesure s’appuie alors sur la métrique de l’espace courbe, ce qui nécessite, du fait de la nature non-linéaire des problèmes engendrés (absence de structure d’espace vectoriel pour ces espaces) de repenser les algorithmes pour la résolution des problèmes d’intérêt en signal et image.
La communauté signal et image s’intéresse depuis quelques années à proposer de nouveaux algorithmes pour le traitement géométrique de l’information (optimisation, estimation, etc.). Ce thème de recherche est dans une phase de maturation avec des applications bien identifiées dans de nombreux domaines (radar, traitement d’images IRM, etc.) et les contributions de la communauté ISIS y sont grandissantes.
Inférence sur variétés
L’inférence statistique a été généralisée à beaucoup de types d’espaces linéaires, mais la transposition des outils d’estimation au cas des espaces non-linéaires est plus compliquée et n’a été abordée que récemment en mathématiques. Dans de nombreux domaines d’application, la matrice de covariance est un objet central à estimer. Dans un contexte de données massives, les observations de taille très importante rendent l’estimation de ces matrices compliquée statistiquement et algorithmiquement. Par exemple, l’écart au modèle gaussien ainsi que le faible nombre d’échantillons soulèvent de nouveaux problèmes. Les lois elliptiques symétriques complexes (CES) permettent de prendre en compte les hétérogénéité des données mais de nombreux problèmes persistent pour caractériser les performances des traitements associés à ces estimateurs. Les méthodes d’optimisation sur variétés peuvent alors permettre de réduire le support d’apprentissage, devenu non convexe par l’inclusion d’information de structure sur la matrice (par exemple Toeplitz, rang faible, Kronecker, etc.).
La multiplication des domaines d’application de ce type de problèmes d’estimation liés aux matrices de covariance empiriques et leur estimation nécessite l’exploration de nouvelles pistes méthodologiques et algorithmiques (convergence, algorithmes rapides).
Traitement du signal sur graphe
Le traitement du signal sur graphe est un axe de recherche récent qui connaît un essor important. Si les applications se multiplient, il reste encore plusieurs verrous identifiés qui monopolisent l’attention de chercheurs de notre communauté. En particulier, il est admis qu’il existe encore un manque d’homogénéité/universalité pour certaines définitions (transformée de Fourier, translation). Plusieurs définitions existent par exemple pour les ondelettes sur graphes, du fait des multiples approches pour définir la translation sur un graphe.
Ce manque d’universalité dans les définitions actuelles engendre l’absence d’algorithmes rapides pour le calcul sur graphes, soulevant des problèmes importantes pour les grandes masses de données. Parmi les autres grandes questions sur lesquelles doit se pencher la communauté signal, trois points semblent particulièrement bloquants : le passage à l’échelle, les aspects liés à la dynamique de graphes et les graphes hétérogènes. Les efforts méthodologiques de la communauté devraient permettre ensuite de démocratiser le traitement du signal sur graphes, et de confirmer les pistes d’applications potentielles prometteuses telles que, parmi d’autres, l’apprentissage et les neurosciences.