Responsables d’axe
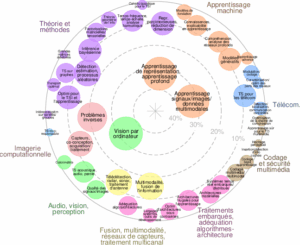
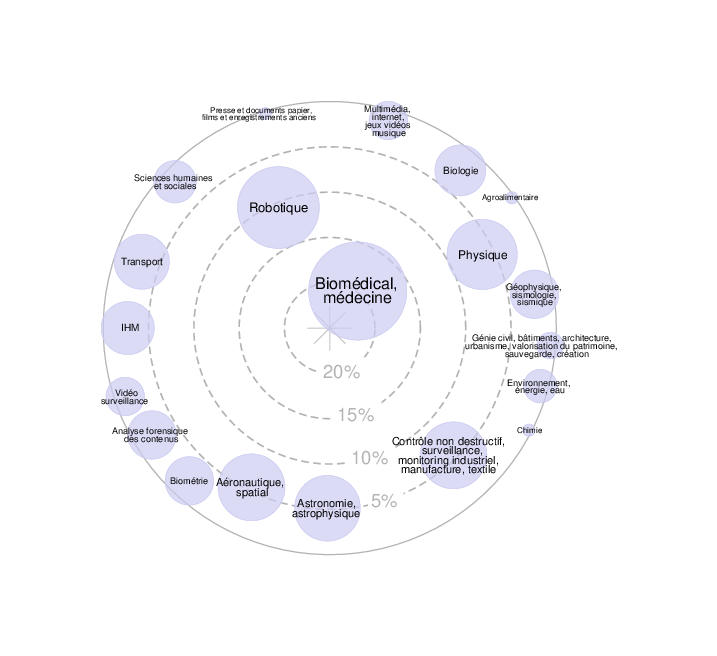
L’axe Théorie et Méthodes a pour objectif d’aider au développement de la recherche théorique en traitement du signal. Les avancées théoriques et méthodologiques en traitement du signal émergent à la fois des besoins nouveaux auxquels le domaine fait face et d’avancées dans des disciplines adjacentes qui ouvrent de nouvelles possibilités.
Contexte
- Volumes croissants de données : C’est une thématique qui a émergé il y a une dizaine d’années mais qui continue de générer des défis pour la recherche. Capteurs de moins en moins coûteux et donc de plus en plus nombreux, activités humaines de plus en plus surveillées et numérisées… Les volumes de données vont croissants.
- Nouveaux besoins en frugalité : La collecte et le traitement de données massives génèrent des dépenses importantes en énergie et une part croissante de la communauté de recherche s’intéresse aux questions de frugalité dans le traitement. Il s’agit ici de concevoir des algorithmes qui sacrifient une part d’efficacité statistique pour augmenter leur efficacité énergétique, qui s’adaptent à des architectures de calcul qui sont moins consommatrices (par exemple, les architectures neuromimétiques), ou encore qui permettent le traitement distribué/fédéré des données pour diminuer les coûts de transmission et de coordination.
- Avancées dans des disciplines adjacentes : Les progrès dans certaines disciplines adjacentes ouvrent des possibilités en traitement du signal, par exemple en apprentissage automatique, optimisation ou en algèbre linéaire numérique.
Exemples de problématiques
- Nouvelles méthodes d’échantillonnage : La théorie de l’échantillonnage, sujet classique du traitement du signal s’il en est, vit actuellement une renaissance. Les nouveaux outils s’appellent sketching, méthode des moments généralisée, échantillonnage adaptatif, coresets et autres. Ces méthodes s’appliquent à des espaces et des types de signaux qui vont bien au-delà de la théorie originale de Shannon. On échantillonne aujourd’hui des signaux sur graphe, sur variété, ou dans des espaces à noyau reproduisant, etc.
- Nouvelles méthodes d’optimisation : Ces dernières années, les progrès théoriques dans ce domaine ont plutôt concerné l’optimisation convexe sur des espaces vectoriels de dimension finie. Or, l’optimisation dans des espaces de dimension infinie (comme par exemple des espaces de mesures) se développe rapidement en ce moment, avec des répercussions intéressantes pour la résolution de problèmes de déconvolution ou dans le domaine du transport optimal. Des progrès sur l’optimisation non-convexe sont également en cours, comme par exemple les méthodes d’homotopie et de monodromie issues de la géométrie algébrique numérique.
- Traitement du signal et statistiques sur variétés : Les statistiques sur variétés Riemanniennes ou la théorie géométrique de la mesure sont deux domaines susceptibles d’interactions riches avec le traitement du signal, qui utilise de plus en plus les espaces non-euclidiens.
- Information et calcul quantique : Le domaine de l’informatique quantique ouvre la voie à des accélérations massives de certains algorithmes, et la communauté en Traitement du Signal s’intéresse à ces nouvelles possibilités.
