Summary
The use of neural networks has recently renewed various fields of mathematical engineering. In particular, the field of weather forecasting has seen the emergence of such numerical weather forecasting models [Lam, 2022], [Kaifeng, 2023]. More generally, deep neural networks (DNN) have opened up new perspectives in the analysis or simulation of physical phenomena governed by partial differential equations (PDE) [Ruthotto & Haber, 2020], [Eliasof, 2021], [Raissi et al., 2019].
A key feature of DNNs is that the mechanisms underlying their predictions are learned from learning data. In a weather forecasting context, a DNN typically predicts future weather conditions from the current state of the atmosphere. Learning its prediction rules is done by comparing predictions to what has been observed in previously acquired real data. A key question to obtain predictions that generalize as well as possible to configurations that are not in the learning base is how to best integrate physical knowledge of the observed phenomena into the prediction rules of neural networks? Several ways exist to answer this question and this internship will explore at least one of them: which new similarity metrics (losses) using to best compare weather predictions to real observations?
The trainee will work on the use of metrics more adapted to weather data than purely local metrics such as standard average-square error losses (MSE). First strategies will be tested by applying the loss functions developed in [Doury, 2022], [Swarcman, 2024] and [Subich, 2025] to the regional weather forecasting system by DNN developed at Météo-France. A more ambitious approach will then be to partially use fundamental equations of weather forecasting models to promote physically consistent predictions. With the help of the supervising team, the trainee will be in charge of understanding the relevance of these equations and interpreting them in the form of similarity metrics for learning.
The tests will be carried out on Météo-France’s Titan dataset https://meteofrance.github.io/ai-lab-blog/weather%20forecasting/machine%20learning/python/dataset/2024/10/24/titan.html. The developments will also be integrated into the ANEMOI package (https://anemoi.readthedocs.io/en/latest/) of the European Centre for Medium-Range Weather Forecasts (ECMWF), which makes it possible to train and infer weather predictions by DNN.
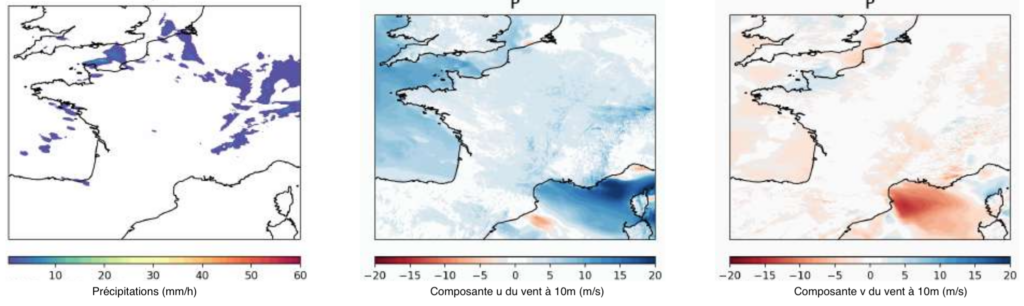
Illustration of the Titan dataset
Profile sought
The trainee will have solid backgrounds in applied mathematics or in physical modeling (PDEs, signal processing, statistics, etc.) and a general knowledge in machine learning. A good experience with Python will be necessary to integrate the strategies developed during the internship into the ANEMOI package. An interest in atmospheric and climate sciences will be a plus. Note that we are ideally looking for a candidate interested in continuing the internship with a PhD thesis.
You can send your CV, recent marks (equivalent M1 and possibly M2), as well as a short cover letter to Laurent Risser (laurent.risser@math.cnrs.fr) to apply.
Bibliography
[Lam, 2022] Lam R et al: GraphCast: Learning skillful medium-range global weather forecasting, Science 382, pp. 1461-1421. 2022
[Kaifeng, 2023] Kaifeng B et al.: Accurate medium-range global weather forecasting with 3D neural networks. Nature 619, pp. 533-538. 2023
[Ruthotto & Haber, 2020] : Deep neural networks motivated by partial differential equations. Journal of Mathematical Imaging and Vision, 62(3), 352–364. 2020
[Eliasof, 2021] Eliasof M. et al.: PDE-GCN: Novel Architectures for Graph Neural Networks Motivated by Partial Differential Equations. Proc NeurIPS. 2021
[Raissi et al., 2019] Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics 378. Pp. 686-707. 2019
[Doury, 2022] Doury A. : PhD thesis: Estimation robuste du changement climatique régional : construction d’une approche hybride entre réseaux de neurones profonds et modèles de climat.
[Swarcman, 2024] Swarcman D. et al: Quantizing reconstruction losses for improving weather data synthesis. Natrue Scientific reports. 2024
[Subich, 2025] Subich et al.: Fixing the Double Penalty in Data-Driven Weather Forecasting Through a Modified Spherical Harmonic Loss Function. arXiv:2501.19374, 2025