Dans le cadre de l’utilisation durable et sûre de l’énergie nucléaire au service de la transition énergétique décarbonée, le réacteur de recherche Jules Horowitz, en cours de construction sur le site du CEA Cadarache, est un outil-clé pour l’étude du comportement des matériaux sous irradiation. Cette ligne d’imagerie présente des caractéristiques extraordinaires de par sa géométrie. En conséquence, certains paramètres d’acquisition indispensables pour la bonne reconstruction de l’image, ne sont pas connus avec précision
L’objectif de ce stage consiste en la proposition et le développement d’un algorithme permettant à la fois la reconstruction de l’image mais également l’estimation des paramètres d’acquisition inconnus. Mathématiquement, le problème est formulé sous la forme d’un problème de minimisation des moindres carrés non-linéaires séparables régularisé, comme suit:
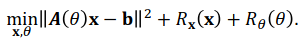
Dans la formule précédente, 𝐱 désigne l’objet à reconstruire à partir des données 𝐛.
L’opérateur 𝑨(𝜃) modélise l’acquisition des données et dépend des paramètres d’acquisition inconnus 𝜃. La particularité de cette formulation réside dans la présence de deux termes de régularisation, un sur l’objet 𝑅𝐱(𝐱) et l’autre sur les paramètres d’acquisition inconnus 𝑅𝜃(𝜃).
La méthode de résolution explorée durant ce stage est une extension de la méthode variable-projection (initialement développée par Golub et Pereyra [1]) basée sur les méthodes primales-duales proximales [2]. En particulier, cette méthode devra être capable de gérer les deux régularisations tout en offrant des garanties de convergence théoriques.
D’un point de vue pratique, la méthode développée devra être capable de reconstruire des objets de grande taille, de l’ordre de quelques giga-octets. Les paramètres à estimer pourront eux aussi être nombreux, de l’ordre de plusieurs centaines. La méthode développée sera intégrée dans la boite à outils Tigre [3], qui offre un cadre performant pour le développement de méthodes de reconstruction tomographiques, avec des fonctions de base optimisées pour GPU.
Enfin, l’efficacité de l’algorithme développé sera validée sur des donnéesexpérimentales. En particulier, différentes fonctions de régularisation seront investiguées afin d’obtenir la meilleure reconstruction d’image possible.
Ce stage sera mené en collaboration avec l’Institut de Mathématiques de Marseille (I2M CNRS 7373, Aix Marseille Université, site Saint Charles). Le stagiaire sera amené, pour ses travaux, à se rendre à l’I2M et au CEA Cadarache. Il ou elle évoluera ainsi au sein de deux environnements stimulants où il/elle pourra développer ses travaux en lien avec des problématiques stratégiques liées au contrôle non destructif.
[1] G. H. Golub and V. Pereyra, Separable nonlinear least squares: the variable projection method and its
applications, Inverse Probl., 19 (2003), pp. R1–R26, https://doi.org/10.1088/0266-5611/19/2/201
[2] A. Repetti, E. Chouzenoux and J. C. Pesquet, Un petit tutoriel sur les méthodes primales-duales proximales pour l’optimisation convexe. Colloque GRETSI (2015). https://hal.science/hal-01379997v1/file/PrimalDual.pdf
[3] A. Biguri, M. Dosanjh, S. Hancock and M. Soleimani, TIGRE: a MATLAB-GPU toolbox for CBCT image
reconstruction. Biomedical Physics & Engineering Express, 2(5):055010, Sept. 2016.
Modalités de candidature
Envoyer CV, lettre de motivation et relevé de notes M1 par mail.
Date limite de candidature
30 Novembre 2025 (Cette date est susceptible d’évoluer en
l’absence de candidatures correspondant au profil recherché.)
- Formation souhaitée
Master 2 ou Diplôme
d’ingénieur en mathématiques
appliquées et/ou en traitement
du signal orienté vers le
machine learning
- Durée du stage
6 mois
- Méthode / logiciel(s)
Programmation Python
- Mots clés
Reconstruction d’images;
Tomographie;
Optimisation;
Méthode primale-duale proximale
- Possibilité de thèse
Oui
- Contacts